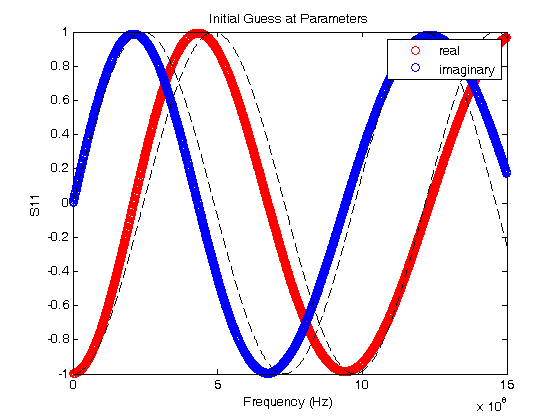
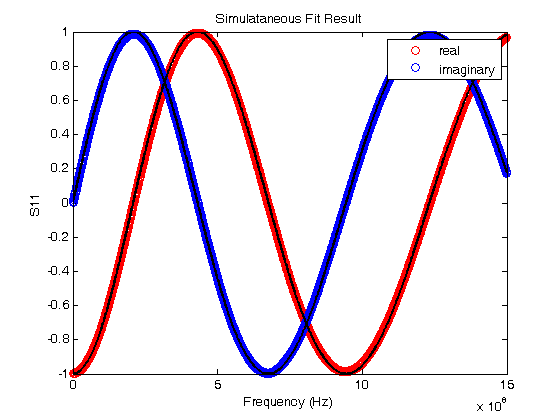
% Jake Bobowsk % July 26, 2017 % Created using MATLAB R2014a clearvars; format longE; % Sometimes a two sets of experimental data depend on the same model % parameters. Consider, for example, the LRC resonator. One could measure % both the magnitude and phase of the voltage across the resistor as a % function of frequency. Both of these quantities depend on the resonant % frequency of the system and a loss parameter. The magnitude and phase % data could be fit independently to determine two sets of the parameters. % Perhaps you could then take a weighted average of the results to produce % a single 'best' value for the resonant frequency and loss parameter. % However, a better approach is to simultaneously fit the two data sets and % directly extract a single best-fit value for each parameter. This % tutorial shows you how to implement a simultaneous fits to multiple data % sets that, each having their own model, but sharing at least some of the % same best-fit parameters. % This tutorial makes use of a MATLAB script called 'nlinmultifit.m' which % was created by Chen Avinadav. I will not make an attempt to explain his % code, but below are the comments provided by the author at the beginning % of his script: %NLINMULTIFIT Nonlinear least-squares regression of multiple data sets % % A wrapper function for NLINFIT which allows simulatenous fitting of % multiple data sets with shared fitting parameters. See example below. % % Unlike different solutions (using fminsearch or similar functions) % this approach enables simple estimation of model predictions and % their confidence intervals, as well as confidence intervals on the % fitted parameters (using the built-in NLPREDCI and NLPARCI functions). % % INPUT: % x_cell,y_cell: Cell arrays containing the x,y vectors of the fitted % data sets. % mdl_cell: Cell array containing model functions for each data set. % beta0: Vector containing initial guess of the fitted parameters. % options: Structure containing control parameters for NLINFIT (see % help file on NLINFIT for more details). % Name,Value pairs: additional options passed to NLINFIT (see help % file on NLINFIT for more details). The 'Weights' % input option may be specified as a cell array, % similar to the input of x_cell and y_cell. % % NOTE: % Unless a cell array of weights is explicitly given, NLINMULTIFIT % will create a weights vector such that all points in all datasets % receive equal weight regardless of each dataset length. % % % OUTPUT: % beta,r,J,Sigma,mse,errorparam,robustw: Direct output from NLINFIT. % % EXAMPLE: % % Generate X vectors for both data sets % x1 = 0:0.1:10; % x2 = 0:1:10; % % % Generate Y data with some noise % y1 = cos(2*pi*0.5*x1).*exp(-x1/5) + 0.05*randn(size(x1)); % y2 = 0.5 + 2*exp(-(x2/5)) + 0.05*randn(size(x2)); % % % Define fitting functions and parameters, with identical % % exponential decay for both data sets % mdl1 = @(beta,x) cos(2*pi*beta(1)*x).*exp(-x/beta(2)); % mdl2 = @(beta,x) beta(4) + beta(3)*exp(-(x/beta(2))); % % % Prepare input for NLINMULTIFIT and perform fitting % x_cell = {x1, x2}; % y_cell = {y1, y2}; % mdl_cell = {mdl1, mdl2}; % beta0 = [1, 1, 1, 1]; % [beta,r,J,Sigma,mse,errorparam,robustw] = ... % nlinmultifit(x_cell, y_cell, mdl_cell, beta0); % % % Calculate model predictions and confidence intervals % [ypred1,delta1] = nlpredci(mdl1,x1,beta,r,'covar',Sigma); % [ypred2,delta2] = nlpredci(mdl2,x2,beta,r,'covar',Sigma); % % % Calculate parameter confidence intervals % ci = nlparci(beta,r,'Jacobian',J); % % % Plot results % figure; % hold all; % box on; % scatter(x1,y1); % scatter(x2,y2); % plot(x1,ypred1,'Color','blue'); % plot(x1,ypred1+delta1,'Color','blue','LineStyle',':'); % plot(x1,ypred1-delta1,'Color','blue','LineStyle',':'); % plot(x2,ypred2,'Color',[0 0.5 0]); % plot(x2,ypred2+delta2,'Color',[0 0.5 0],'LineStyle',':'); % plot(x2,ypred2-delta2,'Color',[0 0.5 0],'LineStyle',':'); % % AUTHOR: % Chen Avinadav % mygiga (at) gmail % % In the example below, the signal reflected (S11) from a short section of % coaxial cable terminated by an inductive loop was measured. S11 has both % real and imaginary components that depend on the same set of parameters. % We will simulataneously fit the real and imaginary parts to their % respective models and extract a single set of best fit parameters. % Import the data and plot it. The data file has three columns: 1. frequency, 2. real % component of S11, and 3. imaginary component of S11. M = dlmread('S11 - real imag.dat'); fdata = M(:,1)'; Sreal = M(:,2)'; Simag = M(:,3)'; plot(fdata, Sreal, 'or'); hold on; plot(fdata, Simag, 'ob'); xlabel('Frequency (Hz)'); ylabel('S11'); title('Initial Guess at Parameters'); legend('real','imaginary') % Here we define some quantities that will be needed. % Z0 is the characteristic impedance of the coaxial cable. % L1 is a guess at the inductance of the loop at the end of the cable % q is a time that is determined by the speed of light, the length of the % coaxial cable, and the dielectric constant of the insulator between the % inner and outer conductors of the cable. Again, I'm making a guess at % its value. % When we do the fits, L1 and q will be the common fit parameters shared by % the models of the real and imaginary parts of the reflection coefficient % S11. Z0 = 50; % ohms L1 = 0.2e-9; % henries q =3.2e-9; % seconds % Xin is an expression for the reactance of the lenght of coaxial cable % terminated by a loop of inductance L1. Xin = Z0*(2*pi*fdata*L1/Z0 + tan(q*fdata))./(1-(2*pi*fdata*L1/Z0).*tan(q*fdata)); % Here are the models for the real and imaginary parts of S11. S11real = ((Xin/Z0).^2-1)./((Xin/Z0).^2+1); S11imag = 2*(Xin/Z0)./((Xin/Z0).^2+1); % Before starting the fit routine, we'll plot the model on top of the data % to see if your guesses at the values of L1 and q are reasonable. If % they're not too bad, we'll use them at the initial parameters at the % start of the fit. plot(fdata, S11real, '--k'); plot(fdata, S11imag, '--k'); hold off; % Let's clear everything and start setting up for the simulataneous fit. clearvars; format longE; % Import the data. M = dlmread('S11 - real imag.dat'); fdata = M(:,1)'; Sreal = M(:,2)'; Simag = M(:,3)'; figure(); plot(fdata,Sreal,'or'); hold on; plot(fdata,Simag,'ob'); xlabel('Frequency (Hz)'); ylabel('S11'); title('Simulataneous Fit Result'); legend('real','imaginary') % To do the fitting, we will rely on the nlinmultifit.m script. The % nlinmultifit.m script must be placed in the same directory as script that % we are currently working in (simultaneous_fits.m) % When we execute nlinmultifit, we will have to pass to it the x and y data % for each of our data sets. We will pass two vectors each for x and y. % These vectors will be stored in "cells". Curly braces are used to % construct cells. In our example, the two datasets have the same x % values, so we enter fdata twice in the x_cell. The y_cell has the real % and imaginary S11 values. If you wanted to simultaneously fit to three % or more datasets, you would just have to enter the correct number of row % vectors in each of the two cells. x_cell = {fdata, fdata}; y_cell = {Sreal, Simag}; % We now define our model functions. % Z0 = 50 ohms is a constant (the characteristic impedance of the coaxial % cable. % f is defined as a variable. It represents frequency, our independent % variable. % Our model will have two parameters: % b(1) = L1 is the inductance of the loop at the end of the coaxial cable. % b(2) = q is a time determined by the length l of the coaxial cable, the % speed of light c, and the dielectric constant e of the insulator filling % the space between the inner and outer conductors [q = 2l/(c/sqrt(e))] Z0 = 50; syms f b = sym('b', [1 2]); % These next few steps are, admittedly, a bit tricky. Like in the nonlinear fit % tutorial, we need to define our fit models as functions. It took me % quite a while to figure out a way to make this work... % First, just enter the models as regular functions. Remember, b(1) % represents L1 and b(2) represents q. Also, any time you need to divide % by a vector or raise a vector to a power, put a dot (.) in front of the % operator. This tells MATLAB that the operation should be performed % element by element rather than using some kind of vector product. % Notice also that I have scaled b(1) by 1e-9. This has been done so that % L1 will be determined in units of nanohenries. b(2) has been scaled by % the same factor so that q will be determined in units of nanoseconds. I % have done this so that b(1) and b(2) will come out to be on the order of % 1 or 10 (0.1 would be okay too). In general, it is good practice to % scale your fit parameters so that they will not be too different. i.e. % you don't want the fit routine to have to deal with one parameter that is % on the order of 1e6 and another that is 1e-12. I always try to get my % fit parameters to come out to be between 0.1 and 10. Xin = Z0*(2*pi*f*b(1)*1e-9/Z0 + tan(b(2)*1e-9*f))./(1-(2*pi*f*b(1)*1e-9/Z0).*tan(b(2)*1e-9*f)); S11real = ((Xin/Z0).^2-1)./((Xin/Z0).^2+1); S11imag = 2*(Xin/Z0)./((Xin/Z0).^2+1); % Here's the bit that took me will to work out... % matlabFunction converts our S11real expression into a function of b1, b2, % and f. Unfortunately, the nonlinear fit routine requirs a function of a % vector b and scalar f. The @(b,f) line converts our function of three % scalars (b1, b2, and f) into a function of vector b and scalar f. b is a % tow-component vector. The first component is b(1) (i.e. L1) and the % second component is b(2) (i.e q). S11Rfcn = matlabFunction(S11real); mdlreal = @(b,f) S11Rfcn(b(1), b(2), f); % Do the same to construct the model function for the imaginary component % of S11. S11Ifcn = matlabFunction(S11imag); mdlimag = @(b,f) S11Ifcn(b(1), b(2), f); % Just like we made cells for the x and y data, we make a cell of the model % functions. mdl_cell = {mdlreal, mdlimag}; % beta0 is vector of initial guesses at the two parameters L1 and q, % respectively. We use the values from the plots that we generated right % at the start of this tutorial. We know that the guesses aren't perfect, % but hopefully they'll be good enough. If not, we'll have to try another % set of guesses... beta0 = [0.2, 3.2]; % In the data used in this tutorial, all data points are going to be % weighted equally (i.e. there's no great variation in the y uncertainties % as frequency is swept). However, in general you would have y % uncertainties for each set of data that would be changing in some way. % In that case, you should define weights for each dataset that are % determined from one over the square of the y uncertainties. Then you % would construct a weights cell. % To demonstrate the use of weights, I define two weights vectors in which % all elements are one, i.e. equally weighted points. Then, I make the % weights cell called w_cell weights1 = ones(1, length(fdata)); weights2 = ones(1, length(fdata)); w_cell = {weights1, weights2}; % Finally, here is where we call nlinmultifit.m to do the simultaneous % fits. To nlinmultifit, we pass x_cell, y_cell, mdl_cell, beta0 (the % initial guess at the parameters), we use the 'Weights' option, and then % pass w_cell. [beta,r,J,Sigma,mse,errorparam,robustw] = ... nlinmultifit(x_cell, y_cell, mdl_cell, beta0, 'Weights', w_cell); % If you didn't want to do a weighted fit, you could just implement nlinmultifit as follows: % [beta,r,J,Sigma,mse,errorparam,robustw] = ... % nlinmultifit(x_cell, y_cell, mdl_cell, beta0); % These next two lines are used to calculate model predictions. [ypred1,delta1] = nlpredci(mdlreal,fdata,beta,r,'covar',Sigma); [ypred2,delta2] = nlpredci(mdlimag,fdata,beta,r,'covar',Sigma); % We can now plot the best-fit results with the original data. plot(fdata,ypred1,'Color','k','LineWidth',2); plot(fdata,ypred2,'Color','k','LineWidth',2); hold off; % The fits look very good! % Here are the calculations of parameter 95% confidence intervals. ci = nlparci(beta,r,'Jacobian',J); % To estimate the best-fit parameters, I take the average of the confidence % bounds. I use have the difference of the confidence bounds to estimate % the uncertainty in the best-fit parameters. L1 = (ci(1,2) + ci(1,1))/2 % nH dL1 = (ci(1,2) - ci(1,1))/2 % nH q = (ci(2,2) + ci(2,1))/2 % ns dq = (ci(2,2) - ci(2,1))/2 % ns % L1 = 11.995 +/- 0.017 nH % q = 2.3131 +/- 0.0007 ns
L1 =
1.199497925822889e+01
dL1 =
1.736682191388006e-02
q =
2.313058330242801e+00
dq =
6.960790543395490e-04