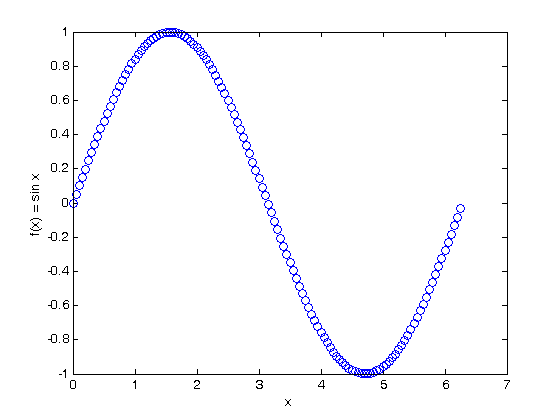
% Jake Bobowski % August 17, 2017 % Created using MATLAB R2014a % This tutorial discusses how to define functions within a MATLAB script. % Once defined, the functions can be evaluated, differentiated, integrated, % plotted, ... Also, if you've taken a look at the nonlinear fitting % tutorial, you'll have seen that model functions that are fit to the data % need to be defined. clearvars % First, we use syms to define the symbolic variable x syms x; % The notation used to define a function is a bit strange. The function % parameters are listed inside @(...), then a space is left before typing % in the form of the function. Here's how to define f to be sin(x). f = @(x) sin(x); % Once defined, it's easy to evaluate the function at any value of x. f(0) f(pi/4) f(pi/2) % We can also take a symbolic derivative of x... diff(f(x), x) % or a symbolic integral... int(f(x), x) % or a definite integral int(f(x), x, 0, pi) % We can also input a vector of x-values and evaluate the function at each % value of x contained in the vector. xx = 0:0.05:2*pi; y = f(xx) % These data can then easily be plotted. plot(xx, y, 'bo') xlabel('x') ylabel('f(x) = sin x') % Here's another simple function: g(x) = x^2. g = @(x) x.^2; % Of course, we can also evaluate this function at any value of x. g(10) % We can also next functions. Here's how to construct sin(x^2)... h = @(x) f(g(x)); % and here's (sin x)^2. l = @(x) g(f(x)); % Can now get MATLAB to apply the chain rule for us. diff(h(x), x) diff(l(x), x) % Everything above was for a function of a single variable. You can, of % course, have a function of any number of variables. Here's a simple % function of two variables: syms y; k = @(x, y) x.^2 + y.^2; k(1, 2)
ans =
0
ans =
0.7071
ans =
1
ans =
cos(x)
ans =
-cos(x)
ans =
2
y =
Columns 1 through 7
0 0.0500 0.0998 0.1494 0.1987 0.2474 0.2955
Columns 8 through 14
0.3429 0.3894 0.4350 0.4794 0.5227 0.5646 0.6052
Columns 15 through 21
0.6442 0.6816 0.7174 0.7513 0.7833 0.8134 0.8415
Columns 22 through 28
0.8674 0.8912 0.9128 0.9320 0.9490 0.9636 0.9757
Columns 29 through 35
0.9854 0.9927 0.9975 0.9998 0.9996 0.9969 0.9917
Columns 36 through 42
0.9840 0.9738 0.9613 0.9463 0.9290 0.9093 0.8874
Columns 43 through 49
0.8632 0.8369 0.8085 0.7781 0.7457 0.7115 0.6755
Columns 50 through 56
0.6378 0.5985 0.5577 0.5155 0.4720 0.4274 0.3817
Columns 57 through 63
0.3350 0.2875 0.2392 0.1904 0.1411 0.0915 0.0416
Columns 64 through 70
-0.0084 -0.0584 -0.1082 -0.1577 -0.2069 -0.2555 -0.3035
Columns 71 through 77
-0.3508 -0.3971 -0.4425 -0.4868 -0.5298 -0.5716 -0.6119
Columns 78 through 84
-0.6506 -0.6878 -0.7232 -0.7568 -0.7885 -0.8183 -0.8460
Columns 85 through 91
-0.8716 -0.8950 -0.9162 -0.9351 -0.9516 -0.9658 -0.9775
Columns 92 through 98
-0.9868 -0.9937 -0.9981 -0.9999 -0.9993 -0.9962 -0.9905
Columns 99 through 105
-0.9825 -0.9719 -0.9589 -0.9435 -0.9258 -0.9058 -0.8835
Columns 106 through 112
-0.8589 -0.8323 -0.8035 -0.7728 -0.7401 -0.7055 -0.6692
Columns 113 through 119
-0.6313 -0.5917 -0.5507 -0.5083 -0.4646 -0.4198 -0.3739
Columns 120 through 126
-0.3271 -0.2794 -0.2311 -0.1822 -0.1328 -0.0831 -0.0332
ans =
100
ans =
2*x*cos(x^2)
ans =
2*cos(x)*sin(x)
ans =
5