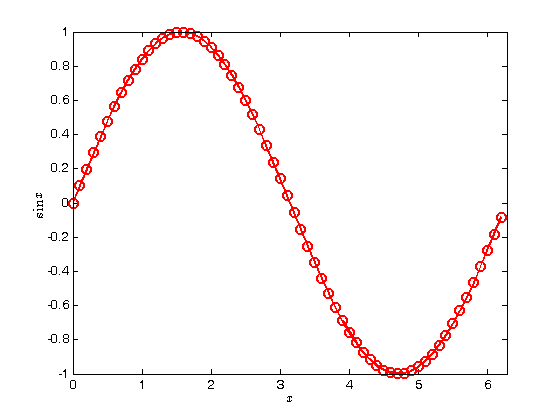
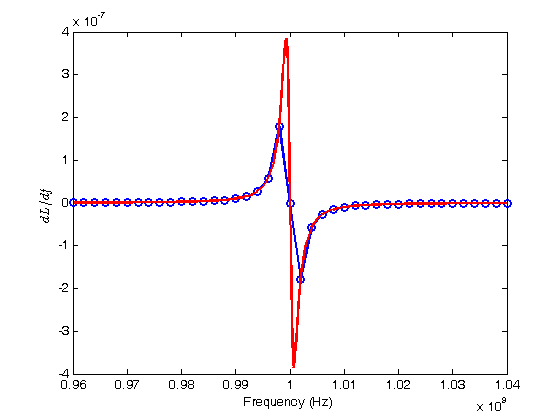
% Jake Bobowski % August 18, 2017 % Created using MATLAB R2014a % The tutorial basic_plots.m discussed how to plot data using 'plot' and % 'errorbar' and then how to format those plots. In this tutorial we plot % functions. Actually, there's no way in MATLAB to give the program a % function and then tell it to plot the function from xi to xf. You % actually have to create a list of x data and then evaluate the function % at all those values of x (thus creating a list of y data) and then plot y % vs x as in basic_plots.m. At first, this might seem odd, but it's % actually not too bad. In fact, it gives you full control of the density % of points to be used in the plots, whereas other prorams will try to % guess for you what might be a good number of points to use. clearvars % Here's a simple example of ploting sin x vs x. First, create some x % data. xx = 0:0.1:2*pi; % Next, create the y data yy = sin(xx); % Finally, create the plot. plot(xx, yy, 'ro-', 'MarkerSize', 8, 'LineWidth', 2) xlabel('$x$', 'Interpreter', 'LaTeX') ylabel('$\sin x$', 'Interpreter', 'LaTeX') axis([0 2*pi -1 1]) % Here's another example. The function plotted below is the frequency % derivative of a Lorentzian. We first define a MATLAB function. syms f f0 Q0; dlorentz = @(f, f0, Q0) (Q0^2./f).*((f0./f).^2 - (f/f0).^2)./((1 + Q0^2*(f/f0 - f0./f).^2).^(3/2)); % The derivative of the Lorentzian has sharp features near the resonance % frequency. First, we show what the plot looks like if we use too few % points. f0 = 1e9; Q0 = 500; ff = [960e6:2e6:1040e6]; figure(); plot(ff, dlorentz(ff, f0, Q0), 'bo-', 'LineWidth', 2) xlabel('Frequency (Hz)') ylabel('$dL/df$', 'Interpreter', 'LaTeX') % Now we use 'hold on' to add a second curve to the figure we just created. % For this second curve we'll use a varying density of points (high density % near the sharp resonant freatures). This results in a much smoother % curve that better represents the true features of the function. hold on; ff = [960e6:2e6:990e6, 990e6:1e6:997e6, 997e6:0.1e6:1003e6, 1003e6:1e6:1010e6, 1010e6:2e6:1040e6]; plot(ff, dlorentz(ff, f0, Q0), 'r-', 'LineWidth', 2) hold off;