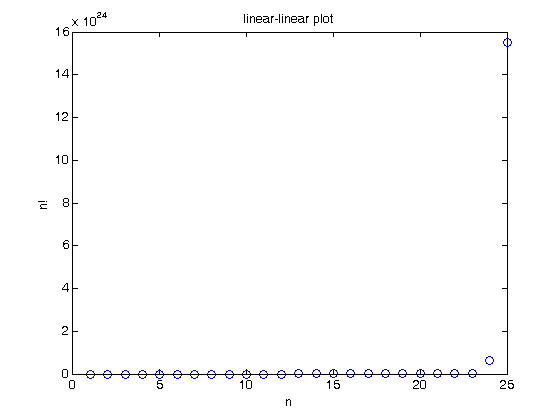
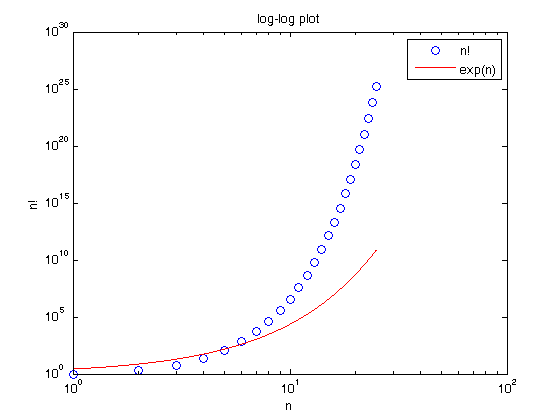
% Jake Bobowski
% July 27, 2017
% Created using MATLAB R2014a

% This tutorial will demonstrate some implementations of nested control
% structures in MATLAB.   Nested structures very quickly become complicated
% and hard to decipher.  It is a very good idea to indent your code so that
% it is easier to read/follow.  MATLAB does a nice job of automatically
% inserting these indentations.

clearvars

% In the while loop tutorial we should how you could calculate factorials
% using while loops.  Suppose you wanted to restrict users to inputing only
% integer values of n.  You can do this by placing your while loop inside
% an if statement.  The if statement will be used to check for valid
% values of n.

% First, I introduce the mod function.  mod(y, x) outputs the modulus of
% y/x.
mod(5, 2)
mod(4, 2)

% We can use mod(n, 1) to check that n is an integer.
mod(5.2, 1)
mod(5, 1)

% So, here is our first nested set of control structures.
n = 4.3;
if mod(n, 1) == 0
    disp(['n = ' num2str(n)])
    factorial = 1;
    while n > 1
        factorial = factorial*n;
        n = n-1;
    end
    disp(['n! = ' num2str(factorial)])
else
    disp(['Invalid entry: n is noninteger.'])
end

% Notice that we can still trick the system into producing nonsense by
% entering a negative integer.
n = -4;
if mod(n, 1) == 0
    disp(['n = ' num2str(n)])
    factorial = 1;
    while n > 1
        factorial = factorial*n;
        n = n-1;
    end
    disp(['n! = ' num2str(factorial)])
else
    disp(['Invalid entry: n is noninteger.'])
end

% To fix this problem, we need to check that n is an integer AND positive.
% We will use && to indicate a logical 'and' in our if statement.  (We
% could use &, but that will evaluate both the lefthand and righthand
% conditions all of the time.  && will only consider the righthand
% condition if the lefthand condition is true.  i.e. && will save some
% computation time is some instances).  We will also implement some elseif
% statements so that we can present proper error messages.

% In the elseif statements ~= means 'not equal to' and <= means 'less than
% or equal to'.  Try different entries for n.  If you enter, for example, a
% string for n you'll get an error message from MATLAB.  As you can see,
% accounting for all the possible silly inputs users could enter tracks a
% lot of though and careful programming!
n = -4.3;
if mod(n, 1) == 0 && n > 0
    disp(['n = ' num2str(n)])
    factorial = 1;
    while n > 1
        factorial = factorial*n;
        n = n-1;
    end
    disp(['n! = ' num2str(factorial)])
elseif n == 0
    disp(['n = ' num2str(n)])
    disp(['n! = 1'])
elseif mod(n, 1) ~= 0 && n > 0
    disp(['Invalid entry: n is noninteger.'])
elseif mod(n, 1) == 0 && n < 0
    disp(['Invalid entry: n negative.'])
elseif mod(n, 1) ~= 0 && n < 0
    disp(['Invalid entry: n is noninteger and negative.'])
end

% Now let's put our factorial code into a for loop so that we can calculate
% n! as a function of n.
start = 0;
finish = 25;
ns = (start:finish);
facts = zeros(finish-start+1, 1)';
for i = start:finish
    n = i;
    if mod(n, 1) == 0 && n > 0
        factorial = 1;
        while n > 1
            factorial = factorial*n;
            n = n-1;
        end
        facts(i + 1) = factorial;
    elseif n == 0
        facts(i + 1) = 1;
    elseif mod(n, 1) ~= 0 && n > 0
        disp(['Invalid entry: n is noninteger.'])
    elseif mod(n, 1) == 0 && n < 0
        disp(['Invalid entry: n negative.'])
    elseif mod(n, 1) ~= 0 && n < 0
        disp(['Invalid entry: n is noninteger and negative.'])
    end
end

% We can now easily make a plot of n! vs n.  Notice how sharply n! rises.
plot(ns, facts, 'bo')
ylabel('n!');
xlabel('n')
title('linear-linear plot')

% Here's the same data on a log-log scale.
figure();
loglog(ns, facts, 'bo')
ylabel('n!');
xlabel('n')
title('log-log plot')
hold on;

% Here, we compare n! to exp(n).  Above about n = 5, n! passes exp(n) and
% continues to increase at a higher rate than exp(n).
xx = (1:0.01:finish);
yexp = exp(xx);
loglog(xx, yexp, 'r-')
legend('n!', 'exp(n)')
hold off;

ans =

     1


ans =

     0


ans =

    0.2000


ans =

     0

Invalid entry: n is noninteger.
n = -4
n! = 1
Invalid entry: n is noninteger and negative.

Published with MATLAB® R2014a