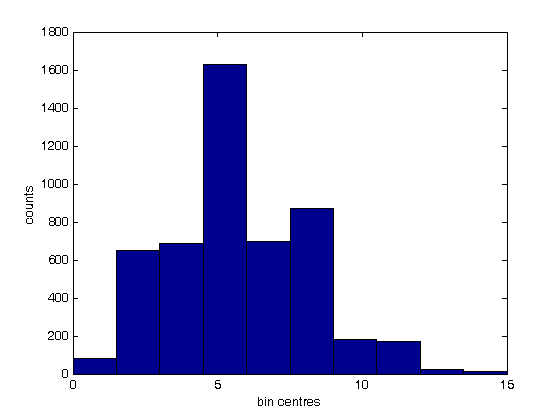
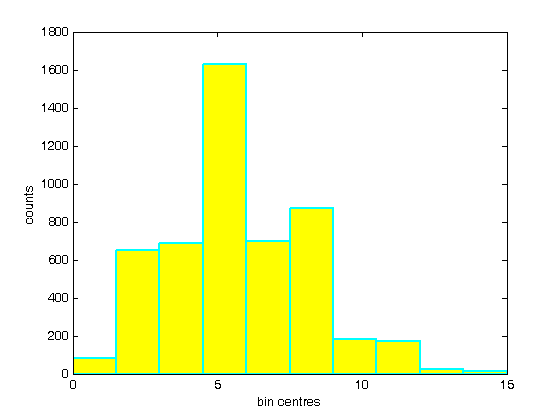
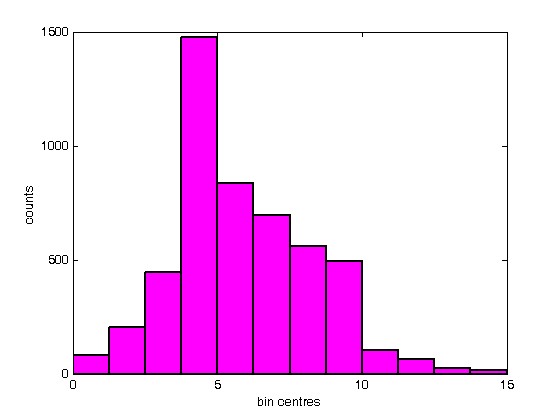
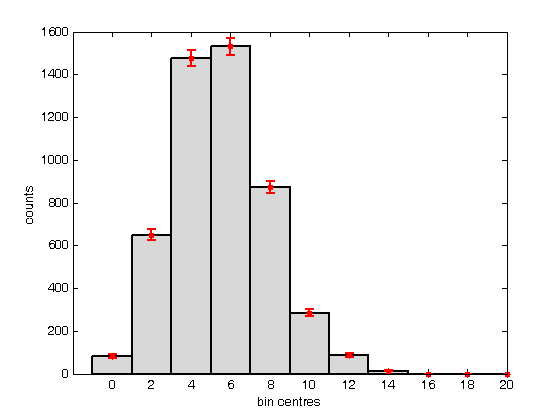
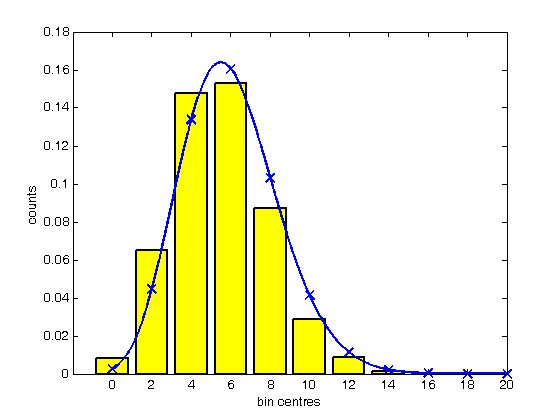
% Jake Bobowski % August 18, 2017 % Created using MATLAB R2014a % This tutorial demonstrates shows how to create histograms in MATLAB. clearvars % First, we create a vector of 5,000 random numbers drawn from a Poisson % distribution. mu = 6; for i = 1:5000 n(i) = poissrnd(mu); end % A histogram can be created simply using 'hist(n)'. % **IMPORTANT** MATLAB says that 'hist' is no longer recommended. They % suggest using 'histogram' instead. However, 'histogram' does not seem % to work in MATLAB 2014a (which I am currently using). If you are working % with a newer version of MATLAB, you may want to try using 'histogram' in % place of 'hist'. hist(n); xlabel('bin centres') ylabel('counts') % I don't understand it, but I looked up how to change to colour of the % bars in the histogram. For what it's worth, here's what I found: figure(); hist(n); xlabel('bin centres') ylabel('counts') set(get(gca, 'child'), 'FaceColor', 'y', 'EdgeColor', 'c', 'LineWidth', 2); % Rather than having hist decide for you, you can specify the number of % bins used to generate the histogram. figure(); nbins = 12; hist(n, nbins); xlabel('bin centres') ylabel('counts') set(get(gca, 'child'), 'FaceColor', 'm', 'EdgeColor', 'k', 'LineWidth', 2); % Instead of specifying the number of bins, you can provide a list of the % bin centres. Notice that I can also specify colours using RGB (red, % green, blue) format. I also called the histogram 'h'. figure(); xbins = [0:2:20]; hist(n, xbins) xlabel('bin centres') ylabel('counts') axis([-2 20 0 1600]) set(get(gca, 'child'), 'FaceColor', [0.85, 0.85, 0.85], 'EdgeColor', 'k', 'LineWidth', 2); % It's worth noting that you can get vectors of the counts in each bin and % the positions of the bin centres of a histogram using: [counts, centres] = hist(n, xbins) % You can also get the bin counts using 'histc'. However, histc is bizarre % in that, to get an aswer that agrees with 'counts' from above, we have to % pass histc the positions of the bin edges, not the bin centres! histc(n, -0.5:2:20.5) % Whatever... it's probably best to just avoid histc altogether. % Now that we have the counts and the bin centres we can, if we want, add a % scatter plot to our histogram. In fact, I chose a Poisson distribution % at the beginning of this script because it arises in counting experiments % and we know that for Poisson distributions the error in the number of % counts in a bin is just the square root of the number of counts. % Hold on... hold on; errorbar(centres, counts, sqrt(counts), 'r.', 'MarkerSize', 16, 'LineWidth', 1.5) hold off; % Here's a way to display multiple histograms in a single plot. figure(); for j = 1:3 for i = 1:2000 m(i, j) = poissrnd(mu); end end hist(m, 0:4:20) xlabel('bin centres') ylabel('counts') axis([-2 20 0 1200]) % Finally, we note that you sometimes may want to normalize your histogram % so that you can put a pdf (Probability Density Function, not Portable % Document Format) on top of it. The probability that an event falls % within a particular bin is given by the number of counts in that bin % (after many many trials), divided by the total number of trials, or the % total number of counts in all bins. Remember, however, that we want to % plot a probability density. That is, we want to plot the probability per % unit x, where x represents whatever quantity is plotted along the x-axis % of the histogram. To get a probability density, we must divide the % number of counts in each bin by the product of the total number of counts % and the bin width. pdfData = counts/(sum(counts)*(xbins(2) - xbins(1))); % We do an easy check to see if we've done things properly. The itegral of % our pdfData should equal one. The integral can be approximated as... sum(pdfData)*(xbins(2) - xbins(1)) % ... and we get a good result. % Now we can make a new, normalized, histogram. This time, we'll use 'bar' % to make our histogram because we no longer have a list of random numbers % that hist wants to use to bin the data an so on. figure(); H = bar(xbins, pdfData, 'FaceColor' , 'y', 'EdgeColor', 'k', 'LineWidth', 2); xlabel('bin centres') ylabel('counts') axis([-2 20 0 0.18]) % We can now add to this plot the expected Poisson pdf using the known mean % of mu = 6 (look way back to the top of this script, line 11). We use % 'poisspdf' to calculate the Poission pdf at the bin centres. Note that % the Poisson distribution is a discrete distribution. That is, it is only % defined for integer values of x. If you try to feed poisspdf noninteger % x-values it will assign zero to the pdf at those values. hold on; y = poisspdf(xbins, mu); plot(xbins, y, 'bx', 'LineWidth', 2, 'MarkerSize', 10); % While poisspdf is technically correct for only outputting nonzero values % at integer x-values, you may, perhaps, wish to show a continuous % representation of the Poisson pdf for aesthetic reasons. Fortunately for % you, some fine members of the MATLAB community has created and shared a % function written to do just that. It's called 'poisson.m'. To use it, % it must be located in the same directory as the script you're using to % call the function. xx = 0:0.01:30; yy = poisson(xx, mu); plot(xx, yy, 'b-', 'LineWidth', 1.5); % So, finally, the above bar graph is our randomly generated Poisson % distribution after it has been scaled to represent a probability density % function (pdf). The points represent the true (discrete) Poisson pdf % using a mean of mu = 6. The line is a continuous representation of the % Poisson pdf. hold off;
counts =
Columns 1 through 6
83 649 1477 1531 873 285
Columns 7 through 11
88 14 0 0 0
centres =
0 2 4 6 8 10 12 14 16 18 20
ans =
Columns 1 through 6
83 649 1477 1531 873 285
Columns 7 through 11
88 14 0 0 0
ans =
1