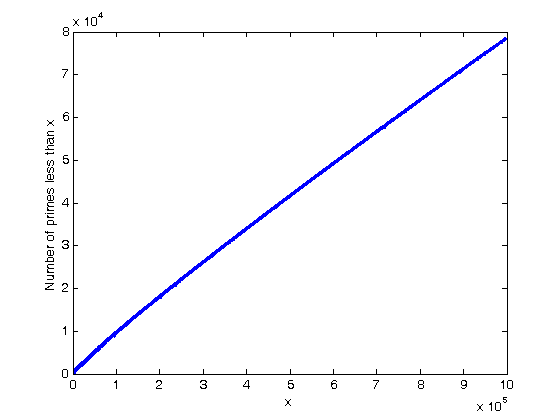
% Jake Bobowski
% August 22, 2016
% Created using MATLAB R2014a

% This tutorial shows how to create a function in MATLAB in one .m file and
% then call and execute that function in another .m MATLAB script.
clearvars
format long;

% The first example function will be used to calculate the factorial of n.
% We will call this function fact and it will be saved in the file fact.m.

% The format for entering this function is shown in the three line below.
% They are commented out in this script, but these lines of code appear in
% the file fact.m.

% function f = fact(n)
%    f = prod(2:n);         % The product of n*(n-1)*(n-2) ... 4*3*2 = n!
% end

% To call an execute this function, the file fact.m must me in the same
% directory as the current script that you're working in.  Then, simply
% enter fact(n) where n is the integer that you want to take the factorial
% of.  Here's the factorial of 5.
fact(5)

% This function (fact(n)) is actually pretty useless because MATLAB already
% has a built-in function to evaluate factorials.
factorial(5)

% Here's another example of a function.  This function will be given a
% vector when called and it will sum the squares of all the elements and
% then take the square root of the sum (so-called adding in quadrature).
% We'll call this function 'quadrature.m'.  Note that this calculation
% could be done using sqrt(sum(n.^2)) where n is the vector.  The for loop
% shown in the commented lines below shows another way of acheiving the
% same result.  These lines have been saved in quadrature.m

% function f = quadrature(n)
%    total = 0;
%    for i = 1:length(n)
%        total = total + n(i)^2;
%    end
%    f = sqrt(total);
% end

% Defining a function like this can save you many lines of code if you need
% to execute this type of calculation over and over again (for example, if
% you're using MATLAB to do a lot of error propagation calculations).
% Below we call the function quadrature(n).
xx = [1, 2, 3];
quadrature(xx)

% As a final example, we'll create a slightly more complicated function.
% This function, called primes.m, will find all of the prime numbers
% between input integers a and b.  The code saved in primes.m is shown
% below without any explanations.  If you open the file primes.m you will
% find some additional comments that help explain the purpose of the
% various line of code.

% function f = primes(a, b) % Start the function.
%     if rem(a, 1) == 0 && rem(b, 1) == 0 && a > 0 && b > 0 && b > a
%         x = 0;
%         for i = a:b
%             cnt = 0;
%             if (i ~= 1 && mod(i, 2) == 1 && mod(sum(int2str(i)-48), 3) ~= 0) && mod(i, 10) ~= 5 || i == 2 || i == 3 || i == 5
%                 j = 7;
%                 while j < i/(j - 2) && cnt == 0
%                     if mod(i, j) == 0
%                         cnt = 1;
%                     end
%                     j = j + 2;
%                 end
%                 if cnt == 0
%                     x = x + 1;
%                     primes(x) = i;
%                 end
%             end
%         end
%         f = primes;
%     else
%         f = 'ERROR: a and b in primes(a, b) must be positive integers with b > a.';
%     end
% end

% We now call the primes(a, b) function.  We have to supply the function
% with the starting and ending integers.
primes(1, 15)
primes(18, 32)

% The function even checks to see if the inputs supplied by the user are
% valid.
primes(-1, 15)
primes(1.1, 15)
primes(15, 1)

% Let's try calling the function with some more interesting inputs.
primes(980, 990)
primes(33456, 33621)
primes(6653332, 6653500)

datestr(clock)
primes(92939223, 92939600)
datestr(clock)
% The function found 16 prime numbers in the vicinity of 90,000,000 in
% less than one second.

% We can use our prime number function to find the number of prime numbers
% between, say, 1 and 1e6 and write those numbers to a file.
max_n = 1e6;
datestr(clock)
x = primes(1, max_n)';
datestr(clock)
length(x)
dlmwrite('primes_1e6.txt', x, 'precision', 12, 'delimiter', '\t');
% This took my laptop about 45 seconds.

% Here's a plot of the number of prime numbers less than x versus x.
plot(x, 1:length(x), 'b-', 'LineWidth', 3)
xlabel('x')
ylabel('Number of primes less than x')

ans =

   120


ans =

   120


ans =

   3.741657386773941


ans =

     2     3     5     7    11    13


ans =

    19    23    29    31


ans =

ERROR: a and b in primes(a, b) must be positive integers with b > a.


ans =

ERROR: a and b in primes(a, b) must be positive integers with b > a.


ans =

ERROR: a and b in primes(a, b) must be positive integers with b > a.


ans =

   983


ans =

  Columns 1 through 6

       33457       33461       33469       33479       33487       33493

  Columns 7 through 12

       33503       33521       33529       33533       33547       33563

  Columns 13 through 18

       33569       33577       33581       33587       33589       33599

  Columns 19 through 22

       33601       33613       33617       33619


ans =

  Columns 1 through 6

     6653351     6653389     6653399     6653411     6653429     6653467

  Column 7

     6653483


ans =

22-Aug-2017 20:01:46


ans =

  Columns 1 through 6

    92939243    92939261    92939299    92939311    92939321    92939377

  Columns 7 through 12

    92939387    92939401    92939453    92939467    92939479    92939501

  Columns 13 through 16

    92939533    92939543    92939563    92939593


ans =

22-Aug-2017 20:01:46


ans =

22-Aug-2017 20:01:46


ans =

22-Aug-2017 20:02:40


ans =

       78498

Published with MATLAB® R2014a