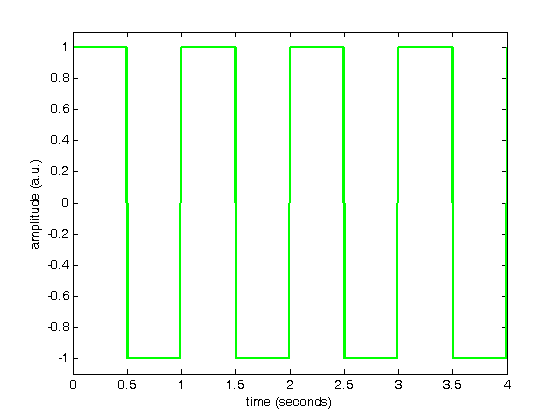
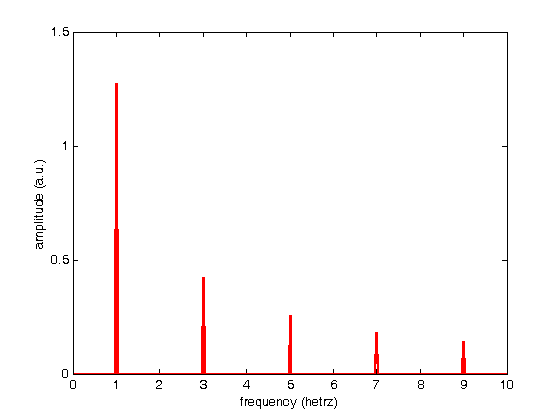
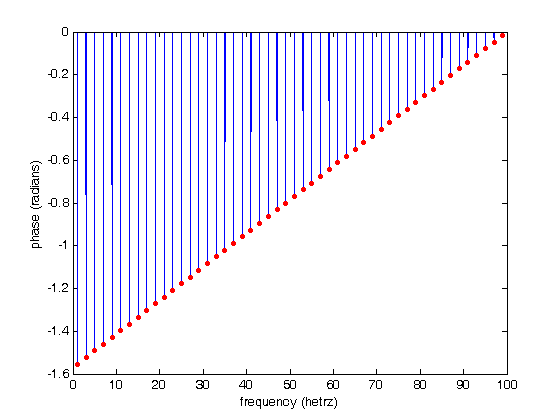
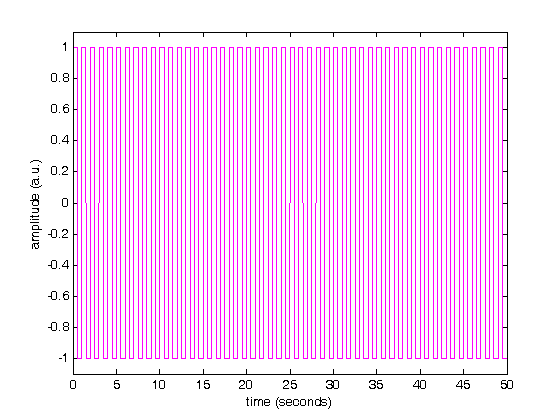
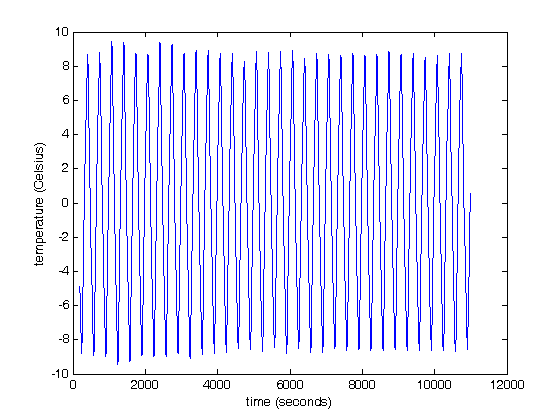
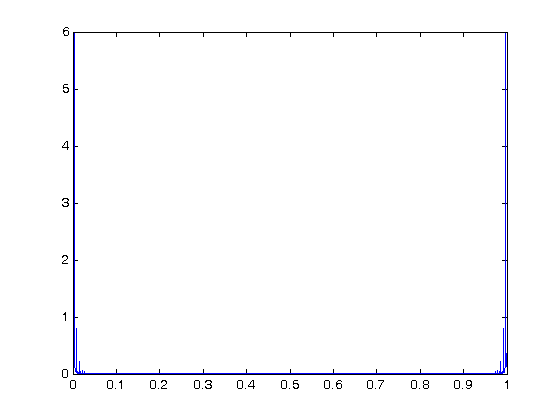
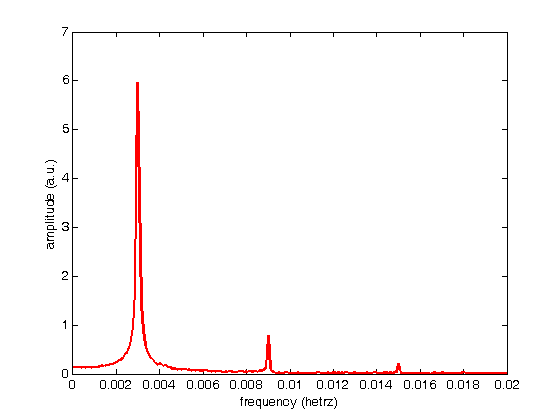
% Jake Bobowski % July 25, 2017 % Created using MATLAB R2014a %Clear all variable assignments. clearvars %Display numbers using scientific notation. format shortE; % In this MATLAB tutorial we show how to compute the Fourier transform (and % inverse Fourier transform) of a set of discrete data using fft (ifft). % FFT stands for Fast Fourier Transform. We will first demonstrate the use % of fft using some artificial data which shows a square wave of amplitude % 1 as a function of time. The period of the square wave is 1 second. The % data is stored in a file called "squareWave.dat". % Import data. square = dlmread('squareWave.dat'); size(square) % Isolate the first column time = square(:,1)'; size(time) length(time) % Here is the second column amplitude = square(:,2)'; % Plot the imported data plot(time,amplitude) axis([0 50 -1.1 1.1]) xlabel('time (seconds)') ylabel('amplitude (a.u.)') % Here's a zoomed-in view of the square wave showing the first few periods. figure() plot(time,amplitude, 'g-', 'LineWidth',2) axis([0 4 -1.1 1.1]) xlabel('time (seconds)') ylabel('amplitude (a.u.)') % Compute the discrete Fourier Transform of the amplitude data using fft. % The fft function outputs a vector of complex numbers. y = fft(amplitude); % The magnitude of the fft can be calculated by adding the squares of the % real and imaginary components (and then taking the square root). The % tangent of the phase is determined by the ratio of the imaginary and real parts. mag = sqrt(real(y).^2 + imag(y).^2); phase = atan(imag(y)./real(y)); % Equivalently, these qunatities can be calculated as follows: m = abs(y); p = angle(y); % We have to determine the appropriate frequency scale for the x-axis. The % maximum frequency is set by the spacing between adjacent times. The % frequency step, is set by fmax/(number of points - 1). fmax = 1/(time(2)-time(1)) fstep = fmax/(length(time)-1) % Therefore the frequency axis is: freq = (0:fstep:fmax); % Below, we plot the magnitude of the fourier transform. I don't know % enough about fft in MATLAB to know why, but the magnitude that is output % is the amplitude of the time signal multiplied by one half the number of % points. To get just the amplitude, I will divided the magnitude by N/2 % before plotting. figure() plot(freq, mag/(length(time)/2)) % Here's a zoomed-in view of the fft magnitude. figure() plot(freq, mag/(length(time)/2), 'r-', 'LineWidth',2) axis([0 10 0 1.5]) xlabel('frequency (hetrz)') ylabel('amplitude (a.u.)') % Notice that the fft shows nonzero frequency components only at the odd % harmonics of the fundamental frequency (1 Hz). Also, the amplitudes % (after removing the N/2 contribution) are correct. One expects the % height of the fundamental frequency component of a square wave of amplitude % 1 to be 4/pi = 1.27. The higher order harmonics should have heights equal % 4/(pi*n) where n = 3, 5, 7, ... % Here's a plot of the phase. figure() plot(freq, p) hold on; plot(freq, phase, 'ro', 'MarkerSize',3, 'MarkerFaceColor', 'r') axis([0 100 -1.6 0]) xlabel('frequency (hetrz)') ylabel('phase (radians)') hold off; % We next verify that the inverse fourier transform ifft works as expected. % If we apply ifft to y, we should recover the original square wave. g = ifft(y); length(g) figure() plot(time, g, 'm-') axis([0 50 -1.1 1.1]) xlabel('time (seconds)') ylabel('amplitude (a.u.)') % All of this works beautifully with artificial (i.e. noiseless) data. In % this last example, we'll import some data from the PHYS 232 thermal waves % experiment and apply the fft routine. The data file that we'll work with % is called "fftdata.dat". % Import data. PHYS232 = dlmread('fftdata.dat'); % Isolate the first column time = PHYS232(:,1)'; % Here is the second column amplitude = PHYS232(:,2)'; % Plot the imported data figure() plot(time,amplitude) xlabel('time (seconds)') ylabel('temperature (Celsius)') % Compute the discrete Fourier Transform of the amplitude data using fft. % The fft function outputs a vector of complex numbers. y = fft(amplitude); m = abs(y); % We have to determine the appropriate frequency scale for the x-axis. The % maximum frequency is set by the spacing between adjacent times. The % frequency step, is set by fmax/(number of points - 1). fmax = 1/(time(2)-time(1)) fstep = fmax/(length(time)-1) % Therefore the frequency axis is: freq = (0:fstep:fmax); % Below, we plot the magnitude of the fourier transform. I don't know % enough about fft in MATLAB to know why, but the magnitude that is output % is the amplitude of the time signal multiplied by one half the number of % points. To get just the amplitude, I will divided the magnitude by N/2 % before plotting. figure() plot(freq, m/(length(time)/2)) % Here's a zoomed-in view of the fft magnitude. figure() plot(freq, m/(length(time)/2), 'r-', 'LineWidth',2) axis([0 0.02 0 7]) xlabel('frequency (hetrz)') ylabel('amplitude (a.u.)') % The fundamental frequency of this data is 0.003 Hz with peaks at the odd % harmonics (0.009 and 0.015 Hz).
ans =
10000 2
ans =
1 10000
ans =
10000
fmax =
200
fstep =
2.0002e-02
ans =
10000
fmax =
1
fstep =
9.2653e-05